
Si la primera derivada de una función es continua en [a,b] se dice que es suave y su gráfica es una curva suave.
Cuando la curva es suave, la longitud de cada pequeño segmentos de recta se puede calcular mediante el teorema de Pitágoras y (dL)2=(dx)2+(dy)2, de tal forma que sumando todos los diferenciales resulta:
Si f es suave en [a,b], la longitud de la curva de f(x) desde a hasta b es:

Suponiendo que se tiene una curva rectificable cualquiera, determinada por una función , y suponiendo que se quiere aproximar la longitud del arco de curva s que va desde un punto a a uno b. Con este propósito es posible diseñar una serie de triángulos rectángulos cuyas hipotenusas concatenadas "cubran" el arco de curva elegido tal como se ve en la figura. Para hacer a este método "más funcional" también se puede exigir que las bases de todos aquellos triángulos sean iguales a Δx, de manera que para cada uno existirá un cateto Δy asociado, dependiendo del tipo de curva y del arco elegido, siendo entonces cada hipotenusa, , al aplicarse el teorema de Pitágoras. Así, una aproximación de s estaría dada por la sumatoria de todas aquellas n hipotenusas desplegadas. Por eso se tiene que:














 , con
, con  , viene dado por la expresión:
, viene dado por la expresión:

 .
. .
. .
. .
. .
.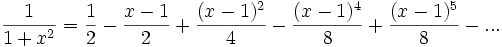
 . Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie
. Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la función a dominio complejo, existe una singularidad en el denominador.La serie .
.